leetcode 1259

问题

You are given an even number of people num_people that stand around a circle and each person shakes hands with someone else, so that there are num_people / 2 handshakes total.

Return the number of ways these handshakes could occur such that none of the handshakes cross.

Since this number could be very big, return the answer mod 10^9 + 7

Example 1:

1
2
Input: num_people = 2
Output: 1

Example 2:

img

1
2
3
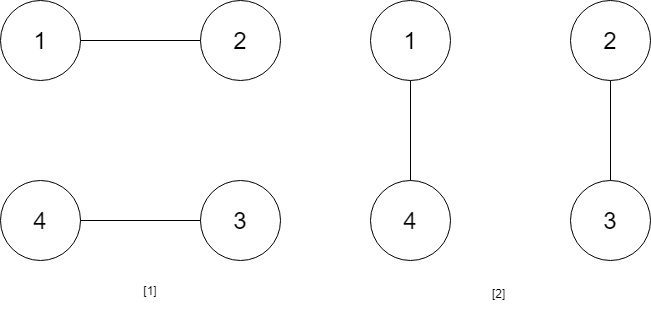
Input: num_people = 4
Output: 2
Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].

Example 3:

img

1
2
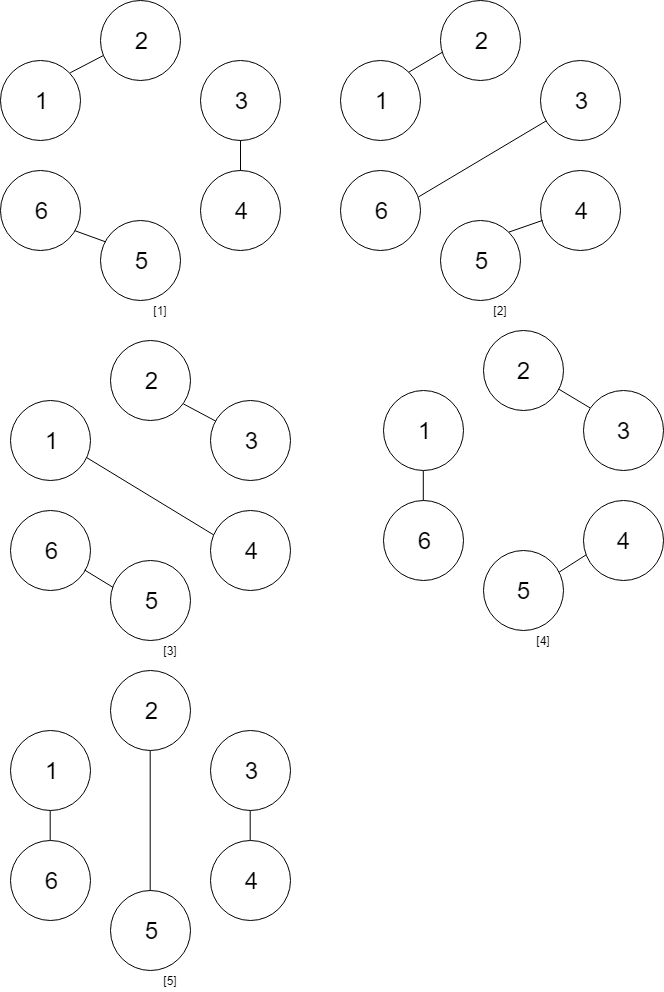
Input: num_people = 6
Output: 5

Example 4:

1
2
Input: num_people = 8
Output: 14

Constraints:

  • 2 <= num_people <= 1000
  • num_people % 2 == 0

分析

思路1: 动态规划

思路2: 卡特兰数

代码1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    const int MOD = 1000000007;
    int numberOfWays(int num_people) {
        vector<long long> dp(num_people+1);
        dp[0] = 1;
        for (int i = 2; i <= num_people; i += 2) {
            dp[i] = 0;
            for (int k = 0; k <= i-2; k += 2) {
                dp[i] = (dp[i] + (dp[k]*dp[i-2-k])%MOD)%MOD;
            }
        }
        return dp[num_people];
    }
};

代码2

1
2
3
4
5
6
7
8
9
10
11
12
13
int numberOfWays(int n) {
    vector<long> inv(n / 2 + 3);
    inv[1] = 1;
    long mod = 1e9 + 7, res = 1;
    for (int i = 2; i < n / 2 + 2; ++i) {
        inv[i] = mod - mod / i * inv[mod % i] % mod;
    }
    for (int i = 1; i <= n / 2; ++i) {
        res = res * (i + n / 2) % mod;
        res = res * inv[i] % mod;
    }
    return res * inv[n / 2 + 1] % mod;
}