leetcode-1391-Check if There is a Valid Path in a Grid

leetcode 1391

问题

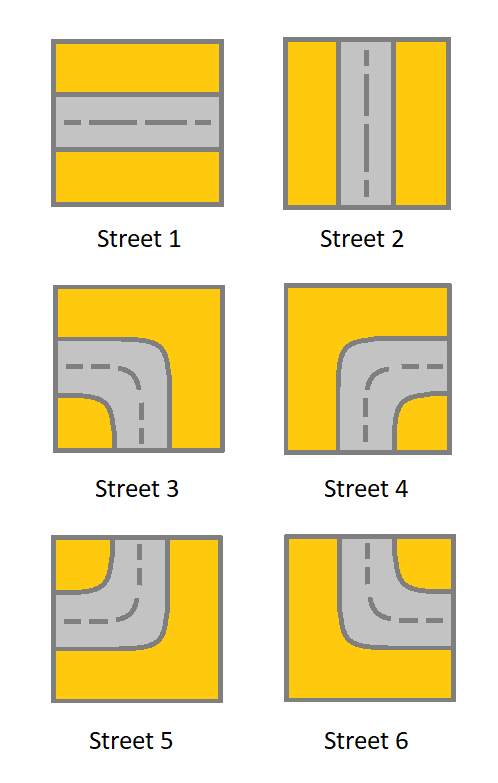
Given a m x n grid. Each cell of the grid represents a street. The street of grid[i][j] can be:

• 1 which means a street connecting the left cell and the right cell.
• 2 which means a street connecting the upper cell and the lower cell.
• 3 which means a street connecting the left cell and the lower cell.
• 4 which means a street connecting the right cell and the lower cell.
• 5 which means a street connecting the left cell and the upper cell.
• 6 which means a street connecting the right cell and the upper cell.

You will initially start at the street of the upper-left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.

Notice that you are not allowed to change any street.

Return true if there is a valid path in the grid or false otherwise.

Example 1:

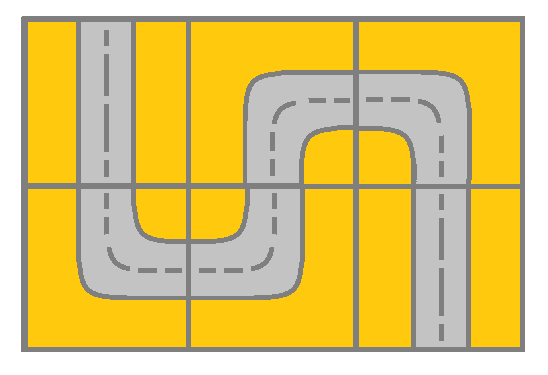
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2:

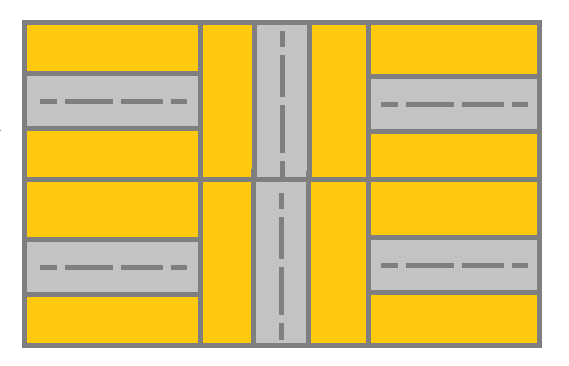
Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3:

Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

Example 4:

Input: grid = [[1,1,1,1,1,1,3]]
Output: true

Example 5:

Input: grid = [[2],[2],[2],[2],[2],[2],[6]]
Output: true

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

分析

使用深度优先搜索，或者广度优先搜索，从坐标 (0, 0) 开始判断是否可达 (m-1, n-1)。这个问题的麻烦点在于，如何判断当前位置是否可以和下一个位置之间联通，单向连通还不行，一定要双向联通。个人的思路是，判断一个位置可以接收到来自哪个方向的输入，比如 street 3，它的上一条的地址可以来自于它的下方和左方。想这样来增加判断条件。rexue70 的方法是，当前位置能够进入到下一个位置，并且下一个位置也能回到当前位置时，才能将下一个的位置判定为有效。

代码1

// DFS
class Solution {
public:
    enum {UP = 0, DOWN, RIGHT, LEFT};
    vector<vector<int>> dirs = {{-1,0}, {1,0}, {0,1}, {0,-1}};
    vector<int> dirsIndex[7] = {
        {},
        {RIGHT, LEFT},
        {UP, DOWN},
        {LEFT, DOWN},
        {RIGHT,  DOWN},
        {LEFT, UP},
        {RIGHT, UP}
    };

    bool hasValidPath(vector<vector<int>>& grid) {
        vector<vector<bool>> canIn(6+1, vector<bool>(4, false));
        canIn[1][RIGHT] = canIn[1][LEFT] = true;
        canIn[2][UP]    = canIn[2][DOWN] = true;
        canIn[3][RIGHT] = canIn[3][UP]   = true;
        canIn[4][LEFT]  = canIn[4][UP]   = true;
        canIn[5][RIGHT] = canIn[5][DOWN] = true;
        canIn[6][LEFT]  = canIn[6][DOWN] = true;

        int m = grid.size();
        int n = m==0? 0: grid[0].size();
        grid[0][0] = -grid[0][0];

        dfs(grid, canIn, 0, 0);

        return grid[m-1][n-1] < 0;
    }

    void dfs(vector<vector<int>>& grid, vector<vector<bool>> &canIn, int x, int y) {
        int m = grid.size();
        int n = grid[0].size();
        int road = abs(grid[x][y]);
        for (int dirOut: dirsIndex[road]) {
            int x_ = x+dirs[dirOut][0];
            int y_ = y+dirs[dirOut][1];
            if (x_ < 0 || x_ >= m || y_ < 0 || y_ >= n || grid[x_][y_] < 0 || canIn[grid[x_][y_]][dirOut] == false)
                continue;

            grid[x_][y_] = -grid[x_][y_];
            dfs(grid, canIn, x_, y_);
        }
    }
};

代码2

class Solution {
public:
    enum {UP = 0, DOWN, RIGHT, LEFT};
    vector<vector<int>> dirs = {{-1,0}, {1,0}, {0,1}, {0,-1}};
    vector<int> dirsIndex[7] = {
        {},
        {RIGHT, LEFT},
        {UP, DOWN},
        {LEFT, DOWN},
        {RIGHT,  DOWN},
        {LEFT, UP},
        {RIGHT, UP}
    };

    bool hasValidPath(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = m==0? 0: grid[0].size();
        queue<pair<int,int>> q;
        q.push({0,0});
        grid[0][0] = -grid[0][0];

        while (q.size() != 0) {
            int x = q.front().first;
            int y = q.front().second;
            q.pop();
            int street = abs(grid[x][y]);
            for (int i: dirsIndex[street]) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                if (nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] < 0)
                    continue;
                for (int j: dirsIndex[grid[nx][ny]]) {
                    if (nx + dirs[j][0] == x && ny + dirs[j][1] == y) {
                        q.push({nx, ny});
                        grid[nx][ny] = -grid[nx][ny];
                    }
                }
            }
        }
        return grid[m-1][n-1] < 0;
    }

};