leetcode 1388

问题

There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:

  • You will pick any pizza slice.
  • Your friend Alice will pick next slice in anti clockwise direction of your pick.
  • Your friend Bob will pick next slice in clockwise direction of your pick.
  • Repeat until there are no more slices of pizzas.

Sizes of Pizza slices is represented by circular array slices in clockwise direction.

Return the maximum possible sum of slice sizes which you can have.

Example 1:

img

1
2
3
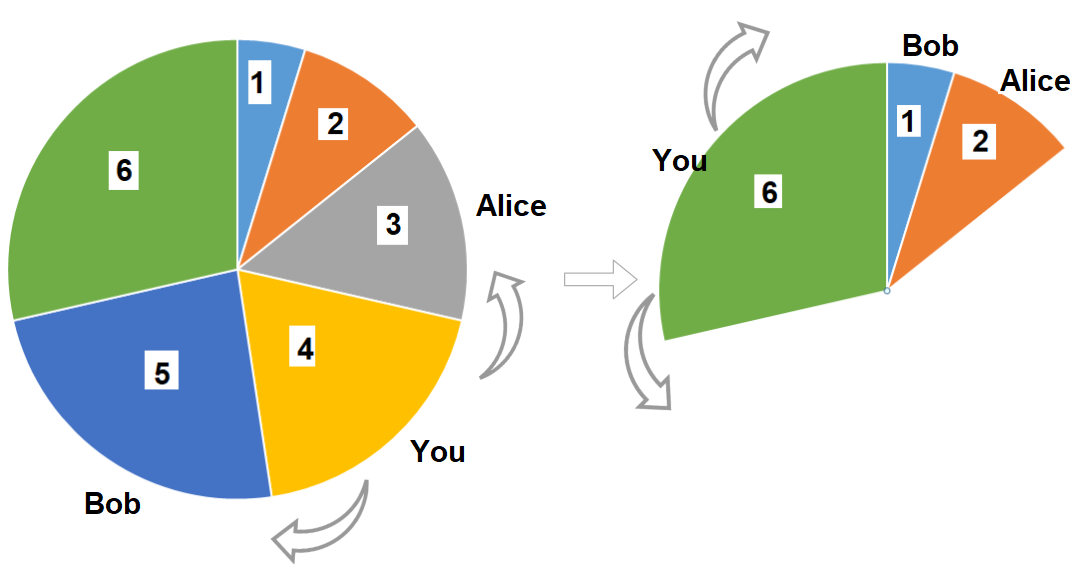
Input: slices = [1,2,3,4,5,6]
Output: 10
Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.

Example 2:

img

1
2
3
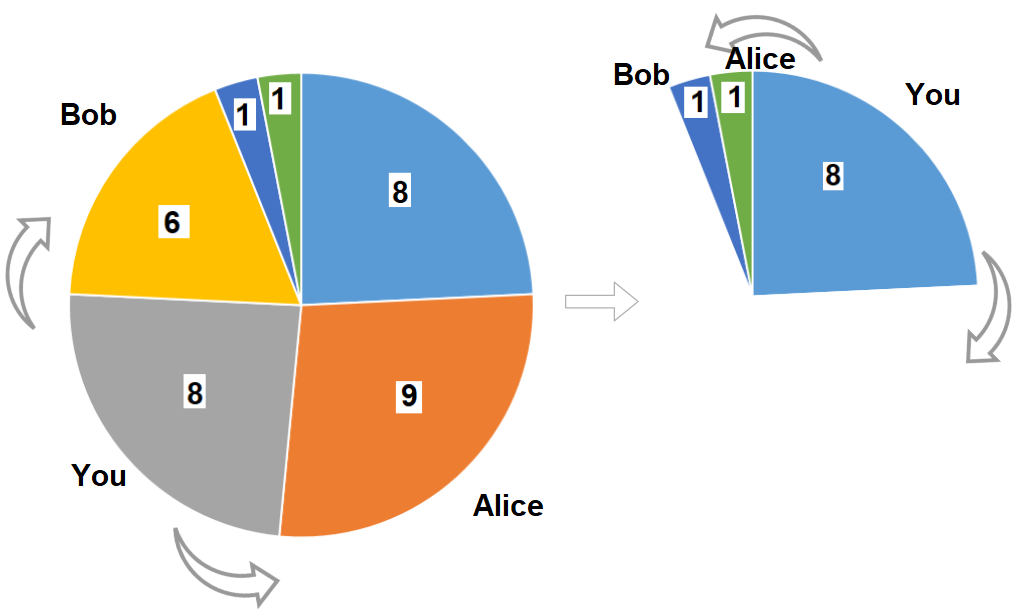
Input: slices = [8,9,8,6,1,1]
Output: 16
Output: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.

Example 3:

1
2
Input: slices = [4,1,2,5,8,3,1,9,7]
Output: 21

Example 4:

1
2
Input: slices = [3,1,2]
Output: 3

Constraints:

  • 1 <= slices.length <= 500
  • slices.length % 3 == 0
  • 1 <= slices[i] <= 1000

分析

该问题可以进行转化，“在一个长度为n数组中，取出 k = n/3 个数，且这k个数不可以俩俩相邻，数组的首尾也算相邻，这k个数的最大和是多少？”，可以很容易地证明，只要这k个数不俩俩相邻那么这k个数就可以满足题意。于是这道题又转化为了一道环形DP问题。我们可以将环断开，分成两个进行求解然后求出两种情况的最大值即可。第一种情况是，永远不会数组中取最后一个数。这样就在vector<int> a2(slices.begin(), slices.end()-1); 中取k个数。第二种情况是永远不会取数组中第一个数，同样，就转化为在vector<int> a1(slices.begin()+1, slices.end()); 避免了判断数组首位成环的情况。对于每一个子问题再假设数组长度为n（原n-1）。令 $dp[i][j]$ 表示在数组 $a[0..j]$ 中最多取 $i$ 个数，所能获得的最大和。对于每个 $j$ 都有取和不取两种情况，则有转移方程如下：
$$
dp[i][j] = max\{ a[i] + dp[i-1][j-2], \;dp[i][j-1]\}
$$
目标：$dp[k][n-1]$

处理好边界条件即可得到结果。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int solve(vector<int> &a, int k) {
        int n = a.size();
        vector<vector<int>> dp(k+1, vector<int>(a.size(), INT_MIN));
        for (int j = 0; j < n; ++j)
            dp[0][j] = 0;
        for (int i = 1; i <= k; ++i)
            dp[i][0] = a[0];
        for (int i = 1; i <= k; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = max(a[j] + (j>=2? dp[i-1][j-2]: 0), dp[i][j-1]);
            }
        }
        return dp[k][n-1];
    }
    int maxSizeSlices(vector<int>& slices) {
        int k = slices.size()/3;
        vector<int> a1(slices.begin()+1, slices.end());
        vector<int> a2(slices.begin(), slices.end()-1);
        return max(solve(a1, k), solve(a2, k));
    }
};