leetcode 309

问题

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

  • You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
  • After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)

Example:

1
2
3
Input: [1,2,3,0,2]
Output: 3 
Explanation: transactions = [buy, sell, cooldown, buy, sell]

分析

思路1: 假设 $DP[i]$ 表示前 $i$ 个交日易能够产生的最大的利润。那么 $DP[i]$ 的计算就有两种情况，第一种情况是在第 $i$ 天没有卖出股票，这个时候 $DP[i] = DP[i-1]$ ，第二种情况是在第 $i$ 天卖出了股票，那么这个时候假设卖出的股票是在第 $j$ 个交易日买入的，那么获得的利润为

$$
DP[i] = \max \limits_{0 \leq j < i} \{preces[i] - prices[j] + dp[j-2]\;(j-2>=0)\}
$$

使用变量 $cache$ 来存储 $prices[j] + dp[j-2] $ 的最小值。时间复杂度 $O(n)$，空间复杂度 $O(n)$。空间复杂度可以优化为 $O(1)$。

思路2: 讨论区好多人似乎并没有思路1中的DP算法，更多的是采用了状态转化这样的一个概念。根据每天所做的动作可以分为三种状态：保持股票（hold），休息（rest），卖出股票（sold），三种动作：观望（do nothing），买入（buy），卖出（sell）。

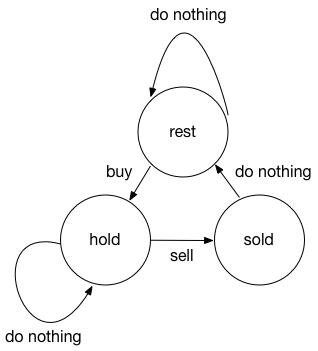
image-20200320154534835

那么整个状态转移可以如上图所示，如hold状态，可以进行的操作有观望和销售，然后分别对应的下一个状态为hold和sold。假设 $rest[i],hold[i],sold[i]$ 分别对应第 $i$ 个交易日在在这三种状态时所能获得的最大利润，则有状态转移方程如下：
$$
hold[i] = max(rest[i-1]-price[i], hold[i-1]) \\
sold[i] = hold[i-1]+price[i] \\
rest[i] = max(rest[i-1], sol d[i-1]) \\
$$
初始状态：int sold = 0, hold = INT_MIN, rest = 0;

目标：max(sold[n-1], rest[n-1]);

经过空间优化之后，时间复杂度 $O(n)$ ，空间复杂度 $O(1)$。

代码1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if (n == 0) return 0;
        vector<int> dp(n, 0);
        dp[0] = 0;
        int cache = prices[0];
        for (int i = 1; i < n; ++i) {
            dp[i] = max(dp[i-1], prices[i] - cache);
            cache = min(cache, prices[i]-(i-2>=0? dp[i-2]: 0));
        }
        return dp[n-1];
    }
};

代码2

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int sold = 0, hold = INT_MIN, rest = 0;
        for (const int &price: prices) {
            int preHold = hold;
            hold = max(hold, rest-price);
            rest = max(rest, sold);
            sold = preHold+price;
        }
        return max(rest, sold);
    }
};