leetcode 1192

问题

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

img

1
2
3
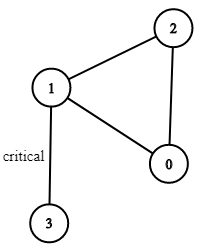
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Constraints:

  • 1 <= n <= 10^5
  • n-1 <= connections.length <= 10^5
  • connections[i][0] != connections[i][1]
  • There are no repeated connections.

分析

通过Tarjan算法求无向图的桥。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    vector<int> dfn, low;
    vector<vector<int>> e;
    int tot;
    void tarjan(int fa, int x, vector<vector<int>> &ans) {
        dfn[x] = low[x] = ++tot;
        for (int y: e[x]) {
            if (y == fa) continue;
            if (dfn[y] != 0) {
                // (x,y) 不是搜索树上的边，仅用来更新回溯值
                low[x] = min(low[x], dfn[y]);
            } else {
                // (x,y)是搜索树树上的边，更新完y的回溯值之后，再判断(x,y)是否是桥
                tarjan(x, y, ans);
                low[x] = min(low[x], low[y]);
                if (dfn[x] < low[y])
                    ans.push_back({x, y});
            }
        }
    }

    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
        dfn = vector<int>(n, 0);
        low = vector<int>(n, 0);
        e = vector<vector<int>>(n);
        tot = 0;

        for (vector<int> &c: connections) {
            e[c[0]].push_back(c[1]);
            e[c[1]].push_back(c[0]);
        }

        vector<vector<int>> ans;
        tarjan(-1, 0, ans);
        return ans;
    }
};