leetcode 1377

问题

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting directly the vertices fromi and toi.

Return the probability that after t seconds the frog is on the vertex target.

Example 1:

img

1
2
3
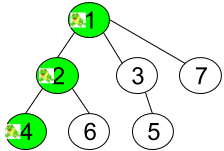
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666 
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.

Example 2:

img

1
2
3
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1.

Example 3:

1
2
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
Output: 0.16666666666666666

Constraints:

  • 1 <= n <= 100
  • edges.length == n-1
  • edges[i].length == 2
  • 1 <= edges[i][0], edges[i][1] <= n
  • 1 <= t <= 50
  • 1 <= target <= n
  • Answers within 10^-5 of the actual value will be accepted as correct.

分析

我们首先可以建立一个图，然后从点1开始使用深度优先搜索找到一条从1到target的路径。然后在求出选出这条路径的概率。

这个题目的carner case要考虑的比较多。

  1. 首先考虑，target就是1的情况，在这种情况下，要么t就是0，或者节点1的度为0才能返回概率1否则返回概率0.

  2. 如果我们经过了k步依然没有到达target，那么达到target的概率是0.

  3. 如果我们在k（k != 0）步之间到达了target，且target的度大于1，则达到target的概率是0.

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
        vector<bool> v(n+1, false);
        vector<vector<int>> e(n+1);
        for (vector<int> &edge: edges) {
            e[edge[0]].push_back(edge[1]);
            e[edge[1]].push_back(edge[0]);
        }
        
        if (target == 1) {
            if (t == 0 || e[1].size() == 0) return 1.0f;
            return 0.0f;
        }
        vector<int> road = {1};
        v[1] = true;
        if (dfs(road, target, v, e, 1) == false || road.size()-1 > t ||
           (road.size()-1<t && e[target].size()>1))
            return 0.0;

        double ans = 1.0f/(e[1].size());
        for (int i = 1; i < road.size()-1; ++i) {
            ans *= 1.0f/(e[road[i]].size()-1);
        }
        
        return ans;
    }

    bool dfs(vector<int> &road, int target, vector<bool> &v, vector<vector<int>> &e, int x) {
        if (x == target)
            return true;
        for (int next: e[x]) {
            if (v[next] == false) {
                road.push_back(next);
                v[next] = true;
                if (dfs(road, target, v, e, next))
                    return true;
                road.pop_back();
                v[next] = false;
                
            }
        }
        return false;
    }
};