leetcode 1373

问题

Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node’s key.
  • The right subtree of a node contains only nodes with keys greater than the node’s key.
  • Both the left and right subtrees must also be binary search trees.

Example 1:

img

1
2
3
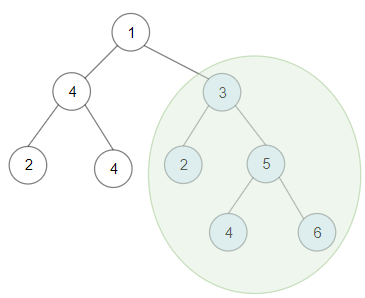
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

Example 2:

img

1
2
3
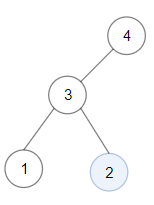
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

1
2
3
Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

Example 4:

1
2
Input: root = [2,1,3]
Output: 6

Example 5:

1
2
Input: root = [5,4,8,3,null,6,3]
Output: 7

Constraints:

  • Each tree has at most 40000 nodes..
  • Each node’s value is between [-4 * 10^4 , 4 * 10^4].

分析

看到树的问题第一反应应该是递归。那么对于一颗子树而言，它是二叉搜索树的条件是：

  1. 左子树为空，或者左子树是二叉搜索树且左子树所有节点中的最大值小于子树的根节点的值。
  2. 右子树为空，或者右子树是二叉搜索树且右子树所有节点中的最小值大于子树的根节点的值。

另外，题目中要求我们求BST的SUM，因此我们递归遍历时需要返回的值就有四个，是否为BST、子树的最小节点值、子树的最大节点值、子树的所有节点的值的综合。我们可以使用一个vector\来依次进行表示。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int ans = 0;
    /* 
    	ret[0]: 是否是BST
    	ret[1]: 节点中的最小值
    	ret[2]: 节点中的最大值
    	ret[3]: 节点中的sum
    */
    vector<int> isBST(TreeNode *root) {
        if (root == NULL)
            return {1, 0, 0, 0};
        vector<int> r = isBST(root->right);
        vector<int> l = isBST(root->left);
        vector<int> ret = {0, root->val, root->val, root->val};
        if (r[0] == 0 || l[0] == 0)
            ret[0] = 0;
        else if ( (root->left == NULL || l[2] < root->val) && 
            (root->right == NULL || r[1] > root->val) ) {
            ret[0] = 1;
            ret[1] = root->left==NULL?  root->val: l[1];
            ret[2] = root->right==NULL? root->val: r[2];
            ret[3] += l[3] + r[3];
            ans = max(ans, ret[3]);
        }
        return ret;
    }
    int maxSumBST(TreeNode* root) {
        isBST(root);
        return ans;
    }
};