Graham扫描法求凸包

算法原理

Graham扫描法的基本思想是通过维护一个凸包候选点的栈S来解决凸包问题。假设现在给定一个二维平面的点集Q，要求其凸包CH(Q)，（CH(Q)表示点集Q的凸包上所有点的集合）。使用Graham扫描法的步骤如下：

找到点集Q中的一个点p0，该点是点集Q中纵坐标（y坐标）最小的点。若纵坐标最小的点有多个，那么p0是这些点中最左边的点，即横坐标（x坐标）最小的点。
将点集Q中除了p0之外剩余的点，按照其与p0的极角（极坐标系下的夹角）从小到大进行排序，设为。若出现有相同极角的情况，则只保留这些极角相同的点中距离p0最远的那一个。（与《算法导论》中所描述的不同，下面实现时，保留了极角相同的点）
若m<2，则所有凸包的候选点不足3个，找不到凸包，返回空。否则进行下一步。
执行循环前，将p0，p1，p2压入栈S中。假设pt表示栈S的栈顶元素，pnt表示栈S中挨着栈顶元素的下一个元素。
执行循环从i=3到m。pi表示当前访问的中的元素（尚未入栈）。
访问每一个元素pi时执行判断。pnt、pt、pi组成的角没有向左转时就将pt弹出栈，再进行判断，直到pnt、pt、pi组成的角向左转时为止。
将pi压入栈。继续执行第5部的循环直到i>m为止。
栈S中从栈底到栈顶以逆时针方向保存着点集Q的凸包CH(Q)中的点。

代码实现

在《算法导论》中给出的例子中，并没有考虑一个凸包中有三点共线的情况。但在很多OJ中，凸包中共线三点的中间点并没有从凸包中去出。因此实现时保留了相同极角的点，以及在循环判断时也考虑了三点共线的情况。在代码实现时主要有两个关键点，一个是按照极角进行排序的算法。第二个是在循环中如何判断“向左转”。

先来看一下按照极角进行排序的算法。假设现在要对两个点a和b按照相对于极点o的极角进行排序。有下面两种方法可以选择。

分别求出两个极角，然后进行比较。极角小的排在前，极角大的排在后。若极角相同，则按照它们相对于点o的距离从小到大进行排序。但是直接求出极角进行比较可能会遇到“浮点数陷阱”的情况。
通过求向量oa、ob的叉乘（向量的外积）来判断，向量oa和ob的位置关系，若oa在ob的顺时针方向则将点a放在点b之前（oaXob > 0）。若向量oa和ob方向相同（oaXob == 0），则按照它们相对于点o的距离从小到大进行排序。

另外，当极角相同判断共线时，由于点o是y坐标最小的点（若有多个y坐标最小的点，o是其中x坐标最小的点），可以直接用点a和点b的纵坐标来代替求oa和ob的长度（若点a和点b的纵坐标也相同则再判断其横坐标）。

对于“向左转”的判断。若角oab“向左转”，则说明向量ab在向量oa的逆时针方向，因此可以使用叉乘来判断。Graham扫描法的原定义以及网上大多数所说的极角相同时按照该点与极点的距离从小到大排序并不适宜凸包含有三点共线的所有情况。如下图中，在对点集进行预处理时按照与最低点（定义为极点）的极角从小到大进行排序，极角相同时按照与极点的距离从小到大排序后再进行扫描处理，最后得到的凸包将不包含[1,2]、[2,1]两个点。

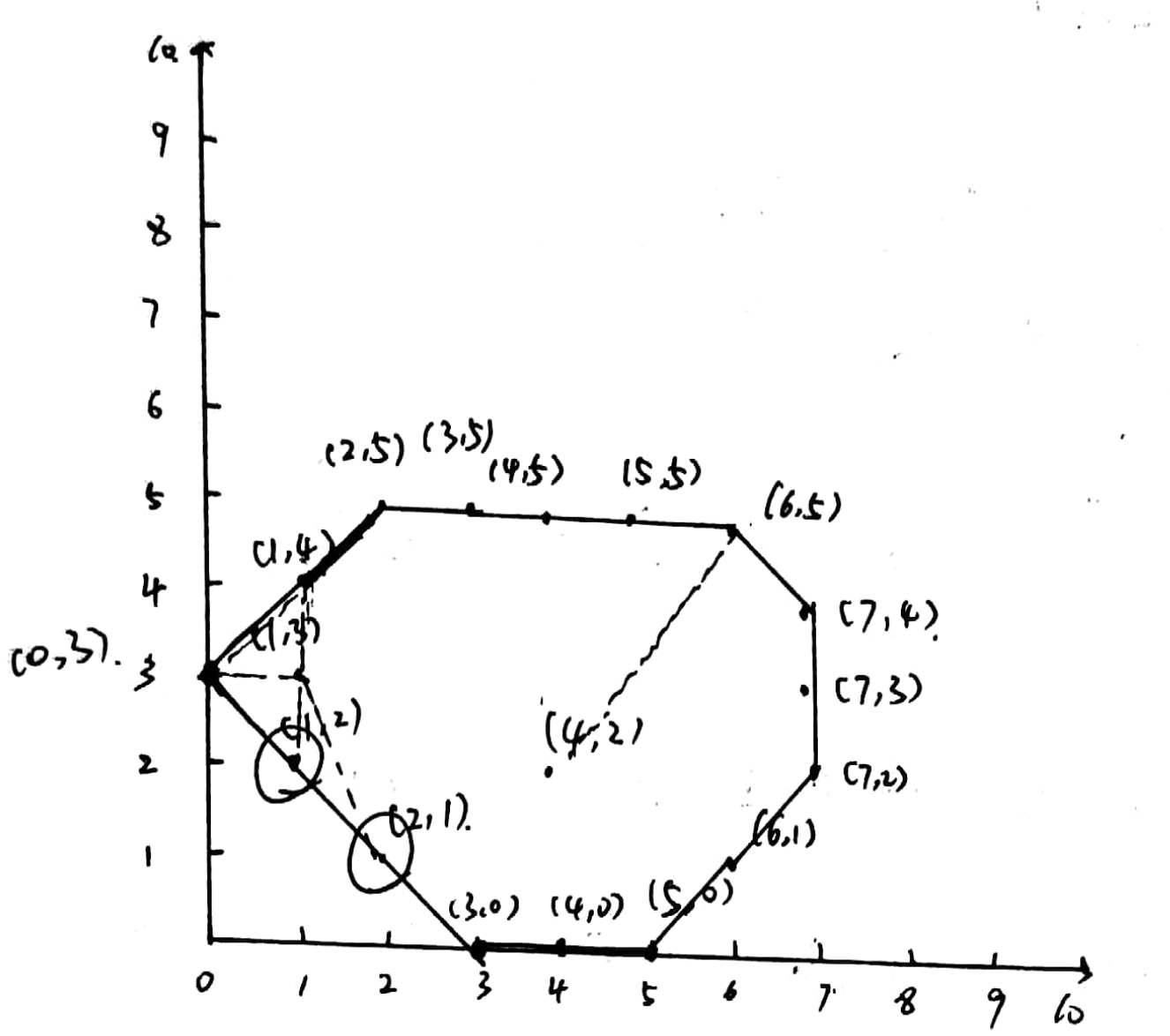
这是因为在最后三个点的处理顺序依次为[2,1]、[1,2]、[0,3]。在处理[0,3]时将会使[2,1]、[1,2]从栈中弹出。要避免这样的情况就需要将极角最大的几个点（若有多个）按照距离从大到小的顺序进行处理。

因此，按照极角从小到大进行排序后的点集，还需要保证点集起始位置极角相同的点要按照与极点的距离从小到大进行排序，点集末尾位置极角相同的点要按照与极点的距离从大到小进行排序。

若非极角最大或者最小的几个极角相同的点，其处理顺序无论是从（按与极点的距离）从小到大还是从大到小都没有影响，因为这些点中只有与极点距离最远的点在凸包中，其余点在这两种处理顺序中都会被弹出栈。

于是CPP源码实现如下。代码用于解决leetcode-587，同时考虑了凸包中有三点共线的情况。

vector <int> o;
// 计算向量ab(x1, y1), cd(x2, y2)的外积 (x1*y2-x2*y1)
int crossProduct(const vector<int> &a, const vector<int> &b,
                const vector<int> &c, const vector<int> &d) {
    int x1 = b[0]-a[0];
    int y1 = b[1]-a[1];
    int x2 = d[0]-c[0];
    int y2 = d[1]-c[1];
    return (x1*y2 - x2*y1);
}

bool comp(const vector<int> &a, const vector<int> &b) {
    int cp = crossProduct(o, a, o, b);
    if (cp > 0)
        return true;
    else if (cp == 0 && (a[1] < b[1] || ((a[1] == b[1] && a[0] < b[0]))))
        return true;

    return false;
}

class Solution {
public:
    void initPoints(vector<vector<int>>& p) {
        int i0 = 0;
        for (int i = 0; i<p.size(); ++i) {
            if (p[i][1] < p[i0][1] || 
               (p[i][1] == p[i0][1] && p[i][0] < p[i0][0]))
                i0 = i;
        }
        swap(p[i0], p[0]);
        o = p[0];
        sort(p.begin()+1, p.end(), comp);
        
        int i = p.size()-2;
        while (i >= 0 && crossProduct(p[0], p.back(), p[0], p[i]) == 0)
            --i;
        
        reverse(p.begin()+i+1, p.end());
    }

    vector<vector<int>> outerTrees(vector<vector<int>>& points) {
        if (points.size() <= 3)
            return points;

        initPoints(points);

        vector <vector<int>> ret;
        ret.push_back(points[0]);
        ret.push_back(points[1]);
        ret.push_back(points[2]);
        
        
        int t = 2; 
        for (int i = 3; i < points.size(); ++i) {
            while (t > 0 && crossProduct(ret[t-1], ret[t], ret[t-1], points[i]) < 0) {
                ret.pop_back();
                t--;
            }
            ret.push_back(points[i]);
            t++;
        }
        
        return ret;
    }
};